Review
Nama: Ariantoly
NIM: 2301877230
Kelas: CB-01
Nama Dosen:
- Henry Chong (D4460)
- Ferdinand Ariandy Luwinda (D4522)
Single Linked List
Single Linked List merupakan Linked List yang hanya terhubung ke data berikutnya.
Fungsi pada Min Heap: find-min, insert, delete-min
Implementasi Min Heap pada Array
Biasakan index 1 dijadikan sebagai root.
Jika current node adalah x, maka
- Parent(x) = x/2
- Left-child(x) = 2*x
- Right-child(x) = 2 * x + 1
Contoh insert
Contoh delete-min (delete 7)
Min-Max Heap
Min-Max Heap memungkinkan kita untuk mendapatkan nilai terbesar dan terkecil sekaligus.
main function
char kata[100] = {"..."};
insert(root, kata);
Find
void find(struct tries *curr, int x){
if(curr->stop == 1){
kata[x] = 0;
printf("%s", kata);
}
for( int i = 0; i < 128 ; i++){
if(curr->edge[i] != 0){
kata[x] = i;
find(curr->edge[i], x+1);
}
}
}
main function
int i, n, oke;
struct tries *curr;
panjang = strlen(kata);
oke = 1;
curr = root;
for(i = 0; i < n && oke == 1; i++){
if(curr->edge[kata[i]] == 0) oke = 0;
else curr = curr->edge[kata[i]];
}
if (oke) find(curr, panjang);
NIM: 2301877230
Kelas: CB-01
Nama Dosen:
- Henry Chong (D4460)
- Ferdinand Ariandy Luwinda (D4522)
Linked List
Pada pertemuan sebelumnya, saya telah mempelajari Single Linked List. Linked List merupakan struktur data yang memanfaatkan dynamic memory allocation dalam membuat sebuah kumpulan data, dan data-data tersebut dihubungkan oleh pointer.
Data-data pada Linked List dapat kita manipulasi dengan insertion (push) dan deletion (pop). Setiap Linked List harus diawali oleh head dan diakhiri oleh tail.
Contoh :
Single Linked List
Single Linked List merupakan Linked List yang hanya terhubung ke data berikutnya.
Codingan dasar dalam membuat Linked List:
struct node {
int nilaiData;
struct node *next;
};
struct node *head = NULL;
struct node *tail = NULL;
Circular Single Linked List
Circular Single Linked List memiliki bentuk yang sedikit berbeda dengan Single Linked List. Tail->next pada Single Linked List menunjukkan nilai NULL, sedangkan pada Circular Single Linked List, tail->next menunjuk pada head. Sehingga tidak terdapat NULL dalam Circular Single Linked List. Dalam codingan, hanya perlu sedikit modifikasi, yaitu dengan mengubah pointer next pada nilai terakhir menunjuk nilai dari head. Hal ini berlaku untuk insertion dan deletion.
Double Linked List
Double Linked List merupakan Linked List yang terhubung dengan data berikutnya dan data sebelumnya.
struct node {
int nilaiData;
struct node *next;
struct node *prev;
};
struct node *head = NULL;
struct node *tail = NULL;
Insertion
Push depan:
1. Membuat node baru (contoh *curr)
2. Mengisi datanya
3. curr->next diisi nilai head dan curr->prev diisi NULL
4. head->prev menjadi curr
5. head menunjuk ke curr
Untuk push belakang, lakukan modifikasi pada node tail.
Untuk push tengah (contoh diantara node x dan node y):
1. Membuat node baru (contoh *curr)
2. Mengisi datanya
3. curr->next menjadi x->next
4. x->next menjadi curr
5. curr->prev menjadi x
6. Ubah prev dari y menjadi curr
Deletion
Terdapat 4 kondisi:
1. Menghapus satu-satunya node dalam Linked List
-> Melepas memori head dan tail
2. Menghapus head dari Linked List
-> Memindahkan head ke data berikutnya, lalu lepas memori head->prev dan beri nilai NULL pada head->prev
3. Menghapus tail dari Linked List
-> Memindahkan tail ke data sebelumnya, lepas memori tail->next, dan beri nilai NULL pada tail->next
4. Menghapus node yang berada di tengah Linked List
-> Cari nilai yang ingin dihapus dengan mengecek nilai next dari node, apabila sudah ditemukan, buat pointer temporary untuk menyimpan nilai dari node yang akan dihapus, dan nilai yang akan ditampung. Contoh a sebagai nilai pertama, del sebagai nilai yang akan dihapus, dan b sebagai nilai kedua. A->next berisi b, dan b->prev berisi a, kemudian lepas memori del.
Circular Double Linked List
Circular Double Linked List berbentuk sirkuit dimana tidak terdapat nilai NULL pada head->prev maupun tail->next. Head->prev berisi nilai tail dan tail->next berisi nilai head.
Review Linked List
Hari ini saya mempelajari codingan dari linked list (push dan pop).
Untuk push, berarti membuat list baru, yang dipelajari kali ini adalah push belakang, baik untuk single linked list maupun double linked list.
struct node{
int value;
struct node *next, *prev;
}*head, *curr, *tail;
void pushBelakangSingle(int value){
curr = (struct node *) malloc(sizeof(struct node));
curr->value = value;
if(head == NULL){
head = tail = curr;
}
else{
tail->next = curr;
tail = curr;
}
curr->next = NULL;
}
Penjelasan (Push Belakang Single Linked List)
Untuk membuat list baru, kita harus memesan memori terlebih dahulu dan memberikan nilai pada node curr. Kemudian, untuk menentukan apakah list ini merupakan list pertama atau bukan, maka kita mengecek apakah head merupakan NULL, jika iya, maka kita tinggal head = tail = curr, karena merupakan list pertama, sehingga secara otomatis, list tersebut merupakan list awal dan list akhir.
Untuk kasus dimana list tersebut bukan list pertama, maka kita cuma perlu membuat tail ke next menunjuk ke nilai curr sekarang, kemudian pindahkan tail ke curr, dan curr (tail yang sekarang) -> next menunjuk NULL.
void pushBelakangDouble(int value){
curr = (struct node *) malloc(sizeof(struct node));
curr->value = value;
if(head == NULL){
head = tail = curr;
head->prev = NULL;
}
else{
tail->next = curr;
curr->prev = tail;
tail = curr;
}
curr->next = NULL;
}
Penjelasan (Push Belakang Double Linked List)
Untuk Double Linked List, sama kita harus memesan memori terlebih dahulu, kasih nilai untuk node curr. Kita juga mengecek apakah head merupakan NULL, untuk melihat apakah ini merupakan list pertama, jika iya, maka head = tail = curr, dan head->prev = NULL, dikarenakan sekarang kita menggunakan double linked list, yang dimana memiliki dua tangan, yaitu next dan prev.
Untuk kasus bukan list pertama, maka kita kasih tail->next menunjuk ke curr, dan curr->prev menunjuk ke tail, kemudian pindahkan tail ke curr, dan curr->next dikasih NULL.
void popBelakang(){
curr = head;
if(head == tail){
head = tail = NULL;
free(head);
}
else{
while(curr->next != tail){
curr = curr->next;
}
free(tail);
tail = curr;
tail->next = NULL;
}
}
Penjelasan (Pop Belakang Single Linked List)
Untuk pop (deletion), kita harus menghapus list-list, yang dimana untuk kali ini merupakan pop belakang. Ketika kita membuat list baru (push), maka posisi curr dan tail biasanya berada pada list paling belakang. Sehingga ketika kita langsung menghapus list paling belakang, maka kita tidak bisa mengembalikan tail ke list paling belakang. Maka dari itu, kita harus memindahkan salah satu (curr atau tail) ke list sebelumnya. Berhubung kasus ini merupakan single linked list, maka kita tidak bisa menggunakan prev untuk mundur. Maka kita harus memindahkan curr ke head, kemudian cari sampai curr berada pada list sebelum tail. Jadi jika curr->next bukan tail, maka kita pindahkan curr ke depan dan dilakukan berulang kali hingga kondisinya salah (curr berada pada list sebelum tail). Setelah itu, kita free memori tailnya, tail nya kita kembalikan ke posisi curr sekarang, yang dimana merupakan list terakhir, dan untuk tail->next nya dikasih NULL, karena sebelumnya tail->next menunjuk pada memori yang telah kita free.
void cetak(){
curr = head;
while(curr!=NULL){
printf("%d\n", curr->value);
curr = curr->next;
}
}
Penjelasan (Mencetak semua single linked list dari head ke tail dengan menggunakan looping)
Untuk mencetak linked list bisa kita gunakan dengan cara manual, namun cara tersebut tidaklah efektif. Maka dari itu, kita memanfaatkan looping untuk mencetak list-listnya. Pertama, kita pindahkan dulu curr ke head. Kemudian, kita cek apakah nilainya NULL, jika bukan kita print. Setelah itu, kita pindahkan curr ke list setelahnya, kemudian kita cek lagi kondisinya, dan dilakukan berulang kali hingga curr berada pada posisi NULL.
Pada pertemuan sebelumnya, saya telah mempelajari Linked List, yang dimana merupakan kumpulan data dinamis yang saling terhubung antar satu sama lain. Terdapat single linked list, double linked list, circular single linked list, dan circular double linked list. Untuk materi kali ini, linked list juga akan terpakai dalam hashing dan binary trees.
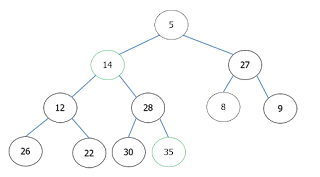
Binary Search Tree merupakan struktur data yang mendukung pencarian dan sorting yang cepat, dan juga memudahkan insertion dan deletion.
Binary Search Tree disebut juga Binary Tree yang sudah disorting.
Dalam sebuah node pada Binary Search Tree:
- Subtree kiri terdiri atas elemen yang lebih kecil
- Subtree kanan terdiri atas elemen yang lebih besar
Operasi dalam Binary Search Tree
- find(x) = menemukan x dalam BST
- insert(x) = memasukkan elemen baru ke dalam BST
- remove(x) = menghapus elemen x dari BST
Operasi: Search
- Mulai pencarian dari root
- Jika root merupakan elemen yang kita cari, maka pencarian selesai
- Jika x lebih kecil root, lakukan pencarian secara rekursif ke bagian kiri sub tree BST, begitu pula jika lebih besar, lakukan pencarian secara rekursif ke bagian kanan sub tree BST. Itu berlaku untuk pencarian ke node berikutnya.
Operasi: Insertion
- Mulai dari root
- Jika x lebih kecil node's key, kemudian masukkan x ke sub tree kiri, jika lebih besar, masukkan x ke sub tree kanan
- Ulangi sampai kita menemukan node kosong untuk diisi
Operasi: Deletion
Terdapat 3 kondisi:
- Jika key merupakan leaf, hapus saja nodenya
- Jika key terdapat dalam node yang mempunyai satu "child", hapus node tersebut dan hubungkan "child"nya dengan "parent"nya
- Jika kunci terdapat dalam node yang mempunyai dua "child", temukan "child" paling kanan dari sub tree kirinya (contoh node x), ubah key yang mau dihapus menjadi key node x, kemudian hilangkan x secara rekursif
Hashing and Hash Table, Trees and Binary Trees
Pada pertemuan sebelumnya, saya telah mempelajari Linked List, yang dimana merupakan kumpulan data dinamis yang saling terhubung antar satu sama lain. Terdapat single linked list, double linked list, circular single linked list, dan circular double linked list. Untuk materi kali ini, linked list juga akan terpakai dalam hashing dan binary trees.
HASHING DAN HASH TABLE
Hashing merupakan teknik mengubah setiap record menjadi angka (hash). Kumpulan dari karakter dalam sebuah record diubah dalam bentuk yang lebih pendek (kata kunci) yang merepresentasikan kumpulan karakter itu sendiri. Keunggulan hashing ini adalah waktu aksesnya yang cukup cepat sehingga waktu yang dibutuhkan dalam penambahan, penghapusan, dan pencarian lebih singkat. Jadi, hashing ini mendistribusikan kunci-kunci dalam sebuah array yang disebut hash table, dengan menggunakan fungsi-fungsi yang disebut hash function.
Contoh hash table:
Misalkan kita ingin menyimpan nama mahasiswa berupa: Doni, Andi, Budi, Fanny, Yadi. Maka, kita dapat mengubah karakter pertama dari setiap string menjadi angka, contohnya a itu 0, b itu 1, c itu 2, sehingga:
HASH FUNCTION
Beberapa cara untuk mengubah string menjadi key:
Mid-square
Mengkuadratkan string/identifier, kemudian mengambil beberapa angka dari hasil kuadrat (dari tengah) untuk dijadikan hash key.
Contoh:
Division
Membagi string/identifier dengan menggunakan operator modulus. Biasanya modulo nya berupa ukuran dari table/array atau menggunakan bilangan prima terdekat diatas banyaknya data.
Contoh:
Diberikan table (array) berukuran 85. Maka kita bisa gunakan 89 sebagai modulo agar setiap hash key itu unik.
Data: ABCD, QWER, ZXCV, ASDF
Gunakan ASCII
ABCD: ((64+1) + (64+2) + (64+3) + (64+4)) % 89 = 88
QWER: ((64+17) + (64+23) + (64+5) + (64+18)) = 52
ZXCV: ((64+26) + (64+24) + (64+3) + (64+22)) = 64
ASDF: ((64+1) + (64+19) + (64+4) + (64+6)) = 19
Folding
Membagi string/identifier menjadi beberapa bagian, kemudian jumlahkan bagian-bagian tersebut untuk mendapatkan hash key.
Digit Extraction
Mengambil bagian dari string/identifier yang diberikan.
Contoh: x = 54321, jika kita mengambil angka ke 2 dan 4, kita akan mendapatkan hash key 24.
Rotating Hash
Biasanya dikombinasikan dengan hash function yang lain (misalnya mid-square atau division). Setelah itu membalikkan urutan angka dari belakang ke depan.
Contoh : Hash key: 24689, Hasil rotasi: 98642
COLLISION
Collision merupakan bentrokan/tabrakan antar hash key, dimana terdapat record yang mempunyai hash key yang sama.
Cara mengatasi collision:
Linear Probing >> Mencari tempat kosong di tempat berikutnya dan letakkan string disana.
Contoh:
Data: Andi, Anton, Caca, Daniel, Ester, Hani, Conan
Cara ini dapat meningkatkan kompleksitas ketika melakukan pencarian.
Chaining >> Meletakkan string dalam slot yang sama menggunakan linked list.
TREES DAN BINARY TREES
Tree merupakan struktur data non linear yang menjelaskan hubugan antar data.
Tree merupakan kumpulan satu node atau lebih.
- Node paling atas disebut "root"
- Node yang tidak memiliki "child" disebut "leaf"
- Node yang memiliki "parent" yang sama disebut "sibling"
- Jika terdapat garis yang menghubungkan node a dan b, maka a merupakan "ancestor" dari b, dan b merupakan "descendant" dari a.
Binary Tree merupakan tree yang dimana setiap node memiliki paling banyak dua "child".
Keterangan (Parent dan Child):
B merupakan "parent" dari D dan E.
D dan E merupakan "child" dari B.
CIRI-CIRI BINARY TREE
Jumlah maksimum node pada setiap level k adalah 2^k.
Jumlah maksimum node dalam sebuah binary tree yang memiliki tinggi h adalah 2^(h+1) - 1
Contoh: h = 4, jumlah maks = 2^4 - 1 = 15.
Tinggi minimum binary tree yang memiliki n nodes adalah 2 log(n).
Tinggi maksimum binary tree yang memiliki n nodes adalah n-1.
PENGAPLIKASIAN BINARY TREE
Implementasi Menggunakan Array
Index 0 adalah node "root".
Index "child" kiri adalah 2p+1, p adalah index "parent"
Index "child" kanan adalah 2p+2, p adalah index "parent"
Index "parent" adalah (p-1)/2
Implementasi Menggunakan Linked List
struct node {
int data;
struct node *left;
struct node *right;
struct node *parent;
};
struct node *root = NULL;
KONSEP EXPRESSION TREE
Prefix: *+/ab-cde
Postfix: ab+cd-e/*
Infix: (a+b) * ((c-d)/e)
Membuat Expression Tree dari Prefix
THREADED BINARY TREE
Dua jenis threaded binary tree:
- Binary Tree with One Way Threading
- Binary Tree with Two Way Threading
Binary Search Tree
Binary Search Tree merupakan struktur data yang mendukung pencarian dan sorting yang cepat, dan juga memudahkan insertion dan deletion.
Binary Search Tree disebut juga Binary Tree yang sudah disorting.
Dalam sebuah node pada Binary Search Tree:
- Subtree kiri terdiri atas elemen yang lebih kecil
- Subtree kanan terdiri atas elemen yang lebih besar
Operasi dalam Binary Search Tree
- find(x) = menemukan x dalam BST
- insert(x) = memasukkan elemen baru ke dalam BST
- remove(x) = menghapus elemen x dari BST
Operasi: Search
- Mulai pencarian dari root
- Jika root merupakan elemen yang kita cari, maka pencarian selesai
- Jika x lebih kecil root, lakukan pencarian secara rekursif ke bagian kiri sub tree BST, begitu pula jika lebih besar, lakukan pencarian secara rekursif ke bagian kanan sub tree BST. Itu berlaku untuk pencarian ke node berikutnya.
Operasi: Insertion
- Mulai dari root
- Jika x lebih kecil node's key, kemudian masukkan x ke sub tree kiri, jika lebih besar, masukkan x ke sub tree kanan
- Ulangi sampai kita menemukan node kosong untuk diisi
Operasi: Deletion
Terdapat 3 kondisi:
- Jika key merupakan leaf, hapus saja nodenya
- Jika key terdapat dalam node yang mempunyai satu "child", hapus node tersebut dan hubungkan "child"nya dengan "parent"nya
- Jika kunci terdapat dalam node yang mempunyai dua "child", temukan "child" paling kanan dari sub tree kirinya (contoh node x), ubah key yang mau dihapus menjadi key node x, kemudian hilangkan x secara rekursif
AVL Tree
AVL Tree merupakan pengembangan dari Binary Search Tree. AVL Tree memberikan kompleksitas yang lebih rendah, khususnya dalam worst case, karena AVL Tree menyeimbangkan root-root dari Binary Search Tree. Dalam melakukan insertion, deletion dan searching, kompleksitasnya sangat dipengaruhi oleh tinggi dari pohon tersebut. Apabila Binary Search Tree memiliki cabang yang cenderung timpang, misal kebanyakan data berada di sisi kiri sementara sisi kanan kosong, itu berpengaruh terhadap kompleksitasnya sendiri. Dan AVL Tree menyelesaikan masalah ini dengan menyeimbangkan cabang-cabangnya sehingga tidak terlalu timpang. Ini yang disebut dengan Balanced Binary Search Tree dan AVL Tree ini merupakan salah satu dari bentuk Balanced Binary Search Tree.
Tinggi sebuah node:
- Tinggi dari sebuah subtree kosong adalah 0
- Tinggi leaf adalah 1
Balance Factor: Perbedaan tinggi antara subtree kiri dan subtree kanan dari sebuah node
*Balance factor sebuah node hanya boleh paling besar 1
Jadi, ketika sebuah node memiliki balance factor lebih dari 1, maka node tersebut dinyatakan melanggar aturan AVL Tree (Violated).
Untuk insertion dan deletion sama aturannya seperti Binary Search Tree, namun untuk AVL Tree ini setelah insert ataupun delete, kita harus memastikan tree dalam kondisi seimbang, jika tidak maka kita harus "Rebalance".
Ada 4 kasus dalam rebalance sebuah Tree:
1. Node paling bawah (dalam insertion merupakan node yang diinsert) berada di bagian kiri dari sub tree kiri node yang dinyatakan violated.
2. Node paling bawah (dalam insertion merupakan node yang diinsert) berada di bagian kanan dari sub tree kanan node yang dinyatakan violated.
3. Node paling bawah (dalam insertion merupakan node yang diinsert) berada di bagian kiri dari sub tree kanan node yang dinyatakan violated.
4. Node paling bawah (dalam insertion merupakan node yang diinsert) berada di bagian kanan dari sub tree kiri node yang dinyatakan violated.
Untuk kasus 1 dan 2 menggunakan single rotation, untuk kasus 3 dan 4 menggunakan double rotation (Dua kali single rotation).
Insertion
Cek parent dari node yang sudah dicek, mulai dari node yang diinsert. Perhatikan balance factornya, jika ada yang menyalahi aturan, maka rebalance.
Single Rotation
Double Rotation
Deletion
Sama seperti insertion, cek satu per satu dari node yang dihapus sampai ke root, kalau ada yang menyalahi aturan balance factor, maka rebalance.
Single Rotation
Double Rotation
HEAP
Heap merupakan complete binary tree dan biasanya diimplementasikan dalam bentuk array, meskipun bisa juga diimplementasikan dalam bentuk linked list.
Aplikasi Heap
- Menemukan nilai terkecil/terbesar, median, dan lain-lain
- Algoritma Dijkstra (Menemukan jalur terpendek dalam graf)
- Algoritma Prim (Menemukan minimum spanning tree)
Min Heap
Setiap node memiliki nilai yang lebih kecil dibandingkan anaknya. Elemen terkecil berada pada root dan elemen terbesar berada pada node leaf.
Fungsi pada Min Heap: find-min, insert, delete-min
Implementasi Min Heap pada Array
Biasakan index 1 dijadikan sebagai root.
Jika current node adalah x, maka
- Parent(x) = x/2
- Left-child(x) = 2*x
- Right-child(x) = 2 * x + 1
Find-min = nilai pada root(index ke-1) karena nilai paling kecil berada pada root.
Insert = Insert elemen baru di posisi akhir (index terakhir) pada heap, kemudian bandingkan node baru tersebut dengan parentnya. Jika current node lebih kecil dari parentnya, swap (tukar posisi) nilai mereka dan lakukan secara rekursif. Proses ini berhenti ketika current node lebih besar dari parentnya atau sudah mencapai root.
- Delete-min = Ambil nilai terakhir pada heap untuk menggantikan nilai pada root, kemudian bandingkan current node (dimulai dari root) dengan nilai anak-anaknya. Swap nilai current node dengan nilai anaknya yang paling kecil dan lakukan secara rekursif. Proses ini berhenti ketika current node lebih kecil dari pada kedua anaknya atau current node merupakan leaf node(tidak memiliki anak).
Insert 20
Insert 5
Contoh delete-min (delete 7)
Max Heap
Setiap nilai node lebih besar dari pada nilai node anaknya. Elemen terbesar berada pada root. Max Heap mirip sama Min Heap, hanya saja berupa kebalikannya.
Min-Max Heap
Min-Max Heap memungkinkan kita untuk mendapatkan nilai terbesar dan terkecil sekaligus.
Di Min-Max Heap, elemen terkecil berada pada root dan elemen terbesar berada pada salah satu child dari root.
Insertion Min-Max Heap
Tambahkan node baru di akhir heap (index terakhir), kemudian:
- Jika node baru berada di level min, apabila parent dari node baru lebih kecil dari node baru, swap nilai kedua node tersebut dan bandingkan lagi current node dengan node grandparent (parent dari parent current node). Jika current node lebih besar dari grandparent, swap nilai kedua node. Namun apabila parent node baru lebih besar atau sama, lakukan yang sebaliknya. Lakukan secara rekursif hingga current node tidak memiliki grandparent.
- Jika node baru berada di level max, apabila parent node baru lebih besar, swap nilai kedua node dan bandingkan dengan grandparentnya. Kalau lebih kecil current nodenya, swap nilai kedua node. Apabila parent node baru lebih kecil lakukan sebaliknya. Lakukan secara rekursif.
Contoh insertion
Insert 50
Insert 5
Deletion Min-Max Heap
Delete elemen terkecil
- Ubah nilai root dengan elemen terakhir
- Kurangi jumlah elemen dalam heap
- Downheapmin dari root
Delete elemen terbesar
- Ubah anak paling besar dari root dengan elemen terakhir
- Kurangi jumlah elemen dalam heap
- Downheapmax dari root
Downheapmin
- Jika x merupakan elemen terkecil dari child atau grandchild current node:
Jika x merupakan grandchild, apabila x lebih kecil dari current node maka swap nilai kedua node (grandchild dan current node) dan apabila sebaliknya, lakukan secara rekursif downheapmin dari x
Jika x merupakan child, apabila x lebih kecil dari current node, maka swap nilai kedua node
Downheapmax: Kebalikan dari downheapmin secara relational operator
Contoh deletion (delete max)
TRIES
Tries merupakan tree tersusun yang biasanya digunakan untuk menyimpan karakter-karakter. Biasanya tries ini digunakan dalam kamus untuk membentuk dan menyusun kata-kata pada kamus. Selain itu, tries juga digunakan dalam auto-text, spell checker, dan lain-lain.
Root pada tries diisi dengan karakter kosong. Untuk setiap kata yang sudah terbentuk harus dikasih penanda stop.
Kata yang bisa dibentuk berdasarkan contoh diatas:
Algo, Api, Bom, Bos, Bosan, Bor
Implementasi Tries pada code
struct tries{
char c;
int stop;
struct tries *edge[128];
} *root = 0;
root = (struct tries *) malloc (sizeof(struct tries));
root->c = '';
root->stop = 0;
Keterangan: c merupakan karakter yang disimpan dalam node, stop sebagai penanda stop dimana jika 1 berarti stop.
Insertion
struct tries* newnode(char huruf){
struct tries* node = (struct tries*) malloc (sizeof(struct tries));
node->c = huruf;
node->stop = 0;
for(int i = 0; i < 128; i++) node->edge[i] = 0;
return node;
}
void insert(struct tries *curr, char *kata){
if(curr->edge[*kata] == 0) curr->edge[*kata] = newnode(*kata);
if(*kata == 0) curr->stop = 1;
else insert(curr->edge[*kata], kata+1);
}
main function
char kata[100] = {"..."};
insert(root, kata);
Find
void find(struct tries *curr, int x){
if(curr->stop == 1){
kata[x] = 0;
printf("%s", kata);
}
for( int i = 0; i < 128 ; i++){
if(curr->edge[i] != 0){
kata[x] = i;
find(curr->edge[i], x+1);
}
}
}
main function
int i, n, oke;
struct tries *curr;
panjang = strlen(kata);
oke = 1;
curr = root;
for(i = 0; i < n && oke == 1; i++){
if(curr->edge[kata[i]] == 0) oke = 0;
else curr = curr->edge[kata[i]];
}
if (oke) find(curr, panjang);



















































Komentar
Posting Komentar