Heaps and Tries

-
HEAP

Heap merupakan complete binary tree dan biasanya diimplementasikan dalam bentuk array, meskipun bisa juga diimplementasikan dalam bentuk linked list.

Aplikasi Heap
- Menemukan nilai terkecil/terbesar, median, dan lain-lain
- Algoritma Dijkstra (Menemukan jalur terpendek dalam graf)
- Algoritma Prim (Menemukan minimum spanning tree)

Min Heap

Setiap node memiliki nilai yang lebih kecil dibandingkan anaknya. Elemen terkecil berada pada root dan elemen terbesar berada pada node leaf.

Fungsi pada Min Heap: find-min, insert, delete-min

Implementasi Min Heap pada Array

Biasakan index 1 dijadikan sebagai root.

Jika current node adalah x, maka
- Parent(x) = x/2
- Left-child(x) = 2*x
- Right-child(x) = 2 * x + 1


Find-min = nilai pada root(index ke-1) karena nilai paling kecil berada pada root.
Insert = Insert elemen baru di posisi akhir (index terakhir) pada heap, kemudian bandingkan node baru tersebut dengan parentnya. Jika current node lebih kecil dari parentnya, swap (tukar posisi) nilai mereka dan lakukan secara rekursif. Proses ini berhenti ketika current node lebih besar dari parentnya atau sudah mencapai root.
- Delete-min = Ambil nilai terakhir pada heap untuk menggantikan nilai pada root, kemudian bandingkan current node (dimulai dari root) dengan nilai anak-anaknya. Swap nilai current node dengan nilai anaknya yang paling kecil dan lakukan secara rekursif. Proses ini berhenti ketika current node lebih kecil dari pada kedua anaknya atau current node merupakan leaf node(tidak memiliki anak).

Contoh insert
Insert 20

Insert 5


Contoh delete-min (delete 7)

Max Heap

Setiap nilai node lebih besar dari pada nilai node anaknya. Elemen terbesar berada pada root. Max Heap mirip sama Min Heap, hanya saja berupa kebalikannya.

Min-Max Heap

Min-Max Heap memungkinkan kita untuk mendapatkan nilai terbesar dan terkecil sekaligus.

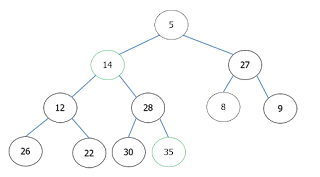
Di Min-Max Heap, elemen terkecil berada pada root dan elemen terbesar berada pada salah satu child dari root.

Insertion Min-Max Heap

Tambahkan node baru di akhir heap (index terakhir), kemudian:
- Jika node baru berada di level min, apabila parent dari node baru lebih kecil dari node baru, swap nilai kedua node tersebut dan bandingkan lagi current node dengan node grandparent (parent dari parent current node). Jika current node lebih besar dari grandparent, swap nilai kedua node. Namun apabila parent node baru lebih besar atau sama, lakukan yang sebaliknya. Lakukan secara rekursif hingga current node tidak memiliki grandparent.
- Jika node baru berada di level max, apabila parent node baru lebih besar, swap nilai kedua node dan bandingkan dengan grandparentnya. Kalau lebih kecil current nodenya, swap nilai kedua node. Apabila parent node baru lebih kecil lakukan sebaliknya. Lakukan secara rekursif.

Contoh insertion

Insert 50


Insert 5



Deletion Min-Max Heap

Delete elemen terkecil
- Ubah nilai root dengan elemen terakhir
- Kurangi jumlah elemen dalam heap
- Downheapmin dari root

Delete elemen terbesar
- Ubah anak paling besar dari root dengan elemen terakhir
- Kurangi jumlah elemen dalam heap
- Downheapmax dari root

Downheapmin
- Jika x merupakan elemen terkecil dari child atau grandchild current node:
  Jika x merupakan grandchild, apabila x lebih kecil dari current node maka swap nilai kedua node (grandchild dan current node) dan apabila sebaliknya, lakukan secara rekursif downheapmin dari x
  Jika x merupakan child, apabila x lebih kecil dari current node, maka swap nilai kedua node

Downheapmax: Kebalikan dari downheapmin secara relational operator

Contoh deletion (delete max)





TRIES

Tries merupakan tree tersusun yang biasanya digunakan untuk menyimpan karakter-karakter. Biasanya tries ini digunakan dalam kamus untuk membentuk dan menyusun kata-kata pada kamus. Selain itu, tries juga digunakan dalam auto-text, spell checker, dan lain-lain.

Root pada tries diisi dengan karakter kosong. Untuk setiap kata yang sudah terbentuk harus dikasih penanda stop.

Kata yang bisa dibentuk berdasarkan contoh diatas:
Algo, Api, Bom, Bos, Bosan, Bor

Implementasi Tries pada code

struct tries{
     char c;
     int stop;
     struct tries *edge[128];
} *root = 0;

root = (struct tries *) malloc (sizeof(struct tries));
root->c = '';
root->stop = 0;

Keterangan: c merupakan karakter yang disimpan dalam node, stop sebagai penanda stop dimana jika 1 berarti stop.

Insertion

struct tries* newnode(char huruf){
     struct tries* node = (struct tries*) malloc (sizeof(struct tries));
     node->c = huruf;
     node->stop = 0;
     for(int i = 0; i < 128; i++) node->edge[i] = 0;
     return node;
}

void insert(struct tries *curr, char *kata){
     if(curr->edge[*kata] == 0) curr->edge[*kata] = newnode(*kata);
     if(*kata == 0) curr->stop = 1;
     else insert(curr->edge[*kata], kata+1);
}

main function
char kata[100] = {"..."};
insert(root, kata);

Find

void find(struct tries *curr, int x){
     if(curr->stop == 1){
          kata[x] = 0;
          printf("%s", kata);
     }
     for( int i = 0; i < 128 ; i++){
          if(curr->edge[i] != 0){
               kata[x] = i;
               find(curr->edge[i], x+1);
          }
     }
}

main function
int i, n, oke;
struct tries *curr;
panjang = strlen(kata);
oke = 1;
curr = root;
for(i = 0; i < n && oke == 1; i++){
     if(curr->edge[kata[i]] == 0) oke = 0;
     else curr = curr->edge[kata[i]];
}
if (oke) find(curr, panjang);














Komentar

Posting Komentar

Postingan populer dari blog ini

AVL Tree

-
Gambar
AVL Tree merupakan pengembangan dari Binary Search Tree. AVL Tree memberikan kompleksitas yang lebih rendah, khususnya dalam worst case, karena AVL Tree menyeimbangkan root-root dari Binary Search Tree. Dalam melakukan insertion, deletion dan searching, kompleksitasnya sangat dipengaruhi oleh tinggi dari pohon tersebut. Apabila Binary Search Tree memiliki cabang yang cenderung timpang, misal kebanyakan data berada di sisi kiri sementara sisi kanan kosong, itu berpengaruh terhadap kompleksitasnya sendiri. Dan AVL Tree menyelesaikan masalah ini dengan menyeimbangkan cabang-cabangnya sehingga tidak terlalu timpang. Ini yang disebut dengan Balanced Binary Search Tree dan AVL Tree ini merupakan salah satu dari bentuk Balanced Binary Search Tree. Tinggi sebuah node: - Tinggi dari sebuah subtree kosong adalah 0 - Tinggi leaf adalah 1 Balance Factor: Perbedaan tinggi antara subtree kiri dan subtree kanan dari sebuah node *Balance factor sebuah node hanya boleh paling besar 1 ...
Baca selengkapnya

Review

-
Gambar
Nama: Ariantoly NIM: 2301877230 Kelas: CB-01 Nama Dosen: - Henry Chong (D4460) - Ferdinand Ariandy Luwinda (D4522) Linked List Pada pertemuan sebelumnya, saya telah mempelajari Single Linked List. Linked List merupakan struktur data yang memanfaatkan dynamic memory allocation dalam membuat sebuah kumpulan data, dan data-data tersebut dihubungkan oleh pointer. Data-data pada Linked List dapat kita manipulasi dengan insertion (push) dan deletion (pop). Setiap Linked List harus diawali oleh head dan diakhiri oleh tail. Contoh : Single Linked List Single Linked List merupakan Linked List yang hanya terhubung ke data berikutnya. Codingan dasar dalam membuat Linked List: struct node { int nilaiData;     struct node *next; }; struct node *head = NULL; struct node *tail = NULL; Circular Single Linked List Circular Single Linked List memiliki bentuk yang sedikit berbeda dengan Single Linked List. Tail->next pada Single L...
Baca selengkapnya

Hashing dan Hash Tables, Trees, dan Binary Trees (Week 4)

-
Gambar
Pada pertemuan sebelumnya, saya telah mempelajari Linked List, yang dimana merupakan kumpulan data dinamis yang saling terhubung antar satu sama lain. Terdapat single linked list, double linked list, circular single linked list, dan circular double linked list. Untuk materi kali ini, linked list juga akan terpakai dalam hashing dan binary trees. HASHING DAN HASH TABLE Hashing merupakan teknik mengubah setiap record menjadi angka (hash). Kumpulan dari karakter dalam sebuah record diubah dalam bentuk yang lebih pendek (kata kunci) yang merepresentasikan kumpulan karakter itu sendiri. Keunggulan hashing ini adalah waktu aksesnya yang cukup cepat sehingga waktu yang dibutuhkan dalam penambahan, penghapusan, dan pencarian lebih singkat. Jadi, hashing ini mendistribusikan kunci-kunci dalam sebuah array yang disebut hash table, dengan menggunakan fungsi-fungsi yang disebut hash function. Contoh hash table: Misalkan kita ingin menyimpan nama mahasiswa berupa: Doni, Andi, B...
Baca selengkapnya